解:
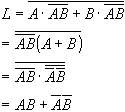 |
结果表明,图1所示电路也是一个同或门。
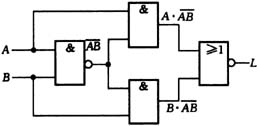 |
| 图1 同或门逻辑电路之一 |
例2 求同或函数的反函数。
解:
上式表明同或函数的反函数为异或函数,它表明两个输入变量取值不同(一个为0,另一个为1)时.输出函数值为1。上面的推导更明确地告诉我们,异或门和同或门互为非函数。所以在异或门电路的输出端再加一级反相器,也能得到同或门,如图2所示。
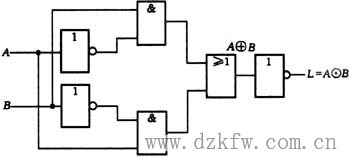 |
| 图2 同或门逻辑电路之二 |
对应同或函数惟一的真值表,已列举出三种不同形式的逻辑表达式和三个逻辑电路,事实上还可以列举许多。由此可以得出结论:一个特定的逻辑问题,对应的真值表是唯一的,但实现它的电路多种多样。我们可以通过函数表达式的变换,使用不同的器件实现相同的逻辑功能。


 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底