通过任意一个闭合曲面的电通量等于包围在该闭合面内所有电荷电量的代数和除以
这个闭合面习惯上叫高斯面。闭合面内的电荷可能有正有负,电量的代数和指的是正负电荷电量的代数和。
2、高斯定理的证明
(1)单个点电荷包围在同心球面内 
设空间有一点电荷![]() ,其周围激发电场。以
,其周围激发电场。以![]() 为球心,
为球心,![]() 为半径作一球面
为半径作一球面![]() 为高斯面。则高斯面上各点场强的大小相等,方向沿矢径方向向外。在高斯面上取一面元
为高斯面。则高斯面上各点场强的大小相等,方向沿矢径方向向外。在高斯面上取一面元![]() ,则通过
,则通过![]() 的电通量为
的电通量为
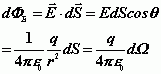
通过整个高斯面的电通量为![]()
(2)单个点电荷包围在任意闭合曲面内
在闭合曲面![]() 内以
内以![]() 为球心,
为球心,![]() 为半径作一任意球面
为半径作一任意球面![]() 为高斯面。在
为高斯面。在![]() 面上取一面元
面上取一面元 ![]() ,则通过
,则通过![]() 的电通量为
的电通量为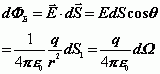
通过整个闭合曲面![]() 的电通量为
的电通量为![]()

以
即![]() 和
和![]() 的数值相等,符号相反,它们的代数和为零。而通过整个闭合曲面的电通量
的数值相等,符号相反,它们的代数和为零。而通过整个闭合曲面的电通量 ![]() 是通过这样一对对面元的电通量之和,因而也等于零。
是通过这样一对对面元的电通量之和,因而也等于零。
(4)多个点电荷的情形 
设空间同时存在![]() 个点电荷,其中
个点电荷,其中![]() 在高斯面 之内,
在高斯面 之内,![]() 在高斯面
在高斯面![]() 之外。设
之外。设![]() 面上任一点的场强为
面上任一点的场强为![]() ,由场强叠加原理,得
,由场强叠加原理,得
![]()
式中![]() 是各点电荷单独存在时的场强。穿过 面的电通量为
是各点电荷单独存在时的场强。穿过 面的电通量为
高斯定理是静电场的两条基本定理之一,它反映了静电场的基本性质:静电场是有源场,"源"即电荷。此外高斯定理不仅对静电场适用,对变化的电场也适用,它是电磁场理论的基本方程之一。



 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底