谐振现象是交流电路中产生的一种特殊现象,对谐振现象的研究有着重要的意义。在实际电路中,它既被广泛地应用,有时又需避免谐振情况发生。
对于无源一端口网络,它的入端阻抗或导纳的值通常与电路频率有关。一个包含有电感和电容的无源一端口网络,其入端阻抗或导纳一般为一复数。但在某些特定的电源频率下,其入端阻抗或导纳的虚部可能变为零,此时阻抗或导纳呈纯电阻特性,使端口电压与电流成为同相。无源一端口网络出现这种现象时称为处于谐振状态。下面分别讨论串联谐振与并联谐振现象。
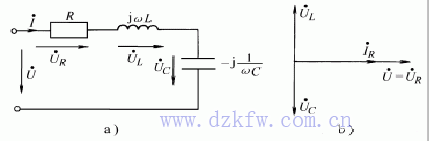
图1
图1为电阻、电感和电容的串联电路,当外施的正弦电压角频率为![]() 时,它的入端阻抗为:
时,它的入端阻抗为:
![]() (1)
(1)
由式可见,RLC串联电路中感抗![]() 与容抗
与容抗![]() 是直接相减的。一般情况下
是直接相减的。一般情况下![]() ,即
,即![]() ,则阻抗的虚部
,则阻抗的虚部![]() 不为零,阻抗角也不为零,此时端电压与电流不同相。当激励电压的角频率变化时,感抗
不为零,阻抗角也不为零,此时端电压与电流不同相。当激励电压的角频率变化时,感抗![]() 与容抗
与容抗![]() 都发生变化。当
都发生变化。当![]() 时,电抗
时,电抗![]() ,电路的入端阻抗
,电路的入端阻抗![]() 为纯电阻。此时电压和电流同相位,电路产生谐振现象。此种电路因为L与C是相串联的,所以称为串联谐振。电路发生串联谐振的条件为电抗值等于零,即
为纯电阻。此时电压和电流同相位,电路产生谐振现象。此种电路因为L与C是相串联的,所以称为串联谐振。电路发生串联谐振的条件为电抗值等于零,即
![]() 或
或 ![]()
电路发生谐振时的角频率称为谐振角频率,用![]() 来表示
来表示
![]() (2)
(2)
电路谐振频率为
![]() (3)
(3)
电路发生谐振时,电路的总电抗![]() ,但感抗
,但感抗![]() 与容抗
与容抗![]() 本身并不为零,它们的值为
本身并不为零,它们的值为
![]() (4)
(4)
![]() 称为谐振电路的特性阻抗,其单位为
称为谐振电路的特性阻抗,其单位为![]() 。
。
电路谐振时,电感电压等于电容电压,且二者相位差为180°,故互相抵消。
![]()
![]()
![]()
![]()
电阻上的压降等于外加电压。电压与电流的相量图如图1b所示。
串联谐振时,电路储存于电感中的磁场能与储存于电容元件中的电场能之间进行能量交换。设外施电压为![]() ,则在串联谐振时,电路中电感电流和电容电压分别为
,则在串联谐振时,电路中电感电流和电容电压分别为
![]()
![]()
此时电感储存的磁场能为:
![]()
电容储存的电场能量为:
![]()
由![]() 可得:
可得:
![]()
可见磁场能与电场能的最大值是相等的。电磁场能量的总和
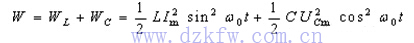
![]()
例1 图3所示电路,已知![]() ,
,![]() ,
,![]() ,求该串联电路的谐振频率
,求该串联电路的谐振频率![]() ,特性阻抗
,特性阻抗![]() 和电路的品质因数Q。
和电路的品质因数Q。
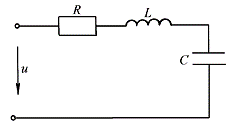
图3
解:电路的谐振角频率
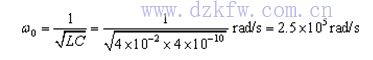
谐振频率
特性阻抗 ![]()
品质因数 ![]()
除了RLC串联谐振电路外,并联RLC谐振电路也被广泛采用。RLC并联谐振电路如图4所示。它的入端导纳为
![]()
由此式可见,当选择
![]()
![]() ,L或C的参数使之满足并联电路的感纳与容纳相等,即
,L或C的参数使之满足并联电路的感纳与容纳相等,即![]() ,
,
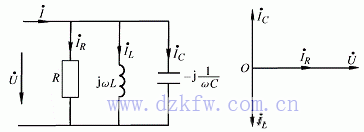
图4
则此时导纳的虚部为零,导纳成为纯电导![]() ,电路入端电压
,电路入端电压![]() 与电流
与电流![]() 相位相同。这种情况就称为RLC并联电路谐振。由上述可知,并联谐振的角频率为
相位相同。这种情况就称为RLC并联电路谐振。由上述可知,并联谐振的角频率为
![]()
并联谐振的条件是感纳与容纳相等![]() ,或
,或![]() 。此时电路入端电流
。此时电路入端电流
![]()
各元件上电流分别为
![]()
![]()
![]()
各电流相量如图4-1-4所示。并联谐振时,若外加电压不变,则谐振时流入的电流最小,此电流等于电阻上流过的电流。电感上无功电流![]() 的幅值与电容上无功电流
的幅值与电容上无功电流![]() 的幅值相等,相位差为
的幅值相等,相位差为![]() ,二者互相抵消,故并联谐振又被称为电流谐振。若并联电路中没有电导G的支路,则谐振时入端导纳
,二者互相抵消,故并联谐振又被称为电流谐振。若并联电路中没有电导G的支路,则谐振时入端导纳![]() ,其等效阻抗
,其等效阻抗![]() ,因此由LC并联而成的电路在发生谐振时,其入端电流
,因此由LC并联而成的电路在发生谐振时,其入端电流![]() 。
。
并联谐振电路的品质因数定义为电路感纳![]() (或容纳
(或容纳![]() )与电导
)与电导![]() 之比,即
之比,即
![]()
品质因数也等于电感电流的幅值(或电容电流的幅值)与流过电阻的电流幅值之比
![]()


 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底