1.齐性定理
齐性定理:在只有一个激励![]() 作用的线性电路中,设任一响应为
作用的线性电路中,设任一响应为![]() ,记作
,记作![]() ,若将该激励乘以常数K,则对应的响应
,若将该激励乘以常数K,则对应的响应![]() 也等于原来响应乘以同一常数, 即
也等于原来响应乘以同一常数, 即![]() 。
。
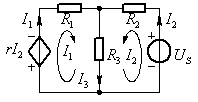
图1 齐性定理示例
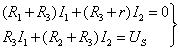 (1)
(1)
当电压源电压改为![]() 时,设回路电流为
时,设回路电流为![]() ,同样可以列得回路电流方程:
,同样可以列得回路电流方程:
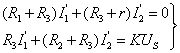 (2)
(2)
另外,如将式(1)各项乘以![]() ,方程仍成立,此时得
,方程仍成立,此时得
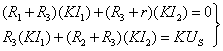 (3)
(3)
方程(2)与(3)是两个系数相同的线性方程组,所以有
![]() ,
,![]()
即回路电流等于原来的![]() 倍。电路中其它响应均可通过回路电流的线性组合而得,所以它们的量值也同样变为原来的
倍。电路中其它响应均可通过回路电流的线性组合而得,所以它们的量值也同样变为原来的![]() 倍。
倍。
例题1:图示电路中电阻![]() 。(1)若使 I0 = 1A,求 US的值。(2)若 US = 66V,求各支路电流。
。(1)若使 I0 = 1A,求 US的值。(2)若 US = 66V,求各支路电流。
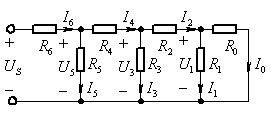
图2 例题1
解: (1)根据KVL、KCL及欧姆定律,由已知电流![]() 依次递推可以求出其它支路电流:
依次递推可以求出其它支路电流:
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
故所需电源电压为:
![]()
(2) 此时相当于将电压源乘以常数![]() ,根据齐性定理,各支路电流均变为原来量值的K倍,即
,根据齐性定理,各支路电流均变为原来量值的K倍,即
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 。
。
2.叠加定理
叠加定理:在线性电路中,由几个独立电源共同作用产生的响应等于各个独立电源单独作用时产生相应响应的代数叠加。
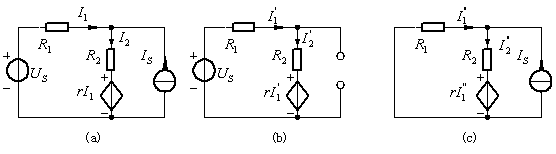
图3 叠加定理示例
解:图(a)电路: 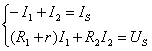
图(b)电路: 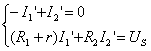
图(c)电路: 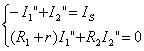
将上面两个方程等号两侧对应项相加,得
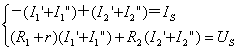
注:1、功率与独立电源的源电压和源电流不是线性关系,所以功率不能直接用叠加关系来计算。
2、线性直流电路的任一响应都是该电路中独立电源的线性组合,即
![]()
例题2: 图4(a)电路,用叠加定理计算电压U。
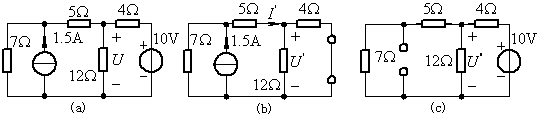
图4 例题2
解: (1)先使独立电流源单独作用,电压源用短路代替,得图(b),计算其中电压![]() 。利用电阻的串、并联等效及分流公式得
。利用电阻的串、并联等效及分流公式得
![]()
![]()
(2)再使独立电压源单独作用,电流源用开路代替,得图(c),计算其中电压![]() 。
。
![]()
(3)根据叠加定理得待求电压
![]()
例题3:图示电路,已知当![]() 时,电压
时,电压![]() 。求当
。求当![]() ,其它条件不变时电压U的值。
,其它条件不变时电压U的值。
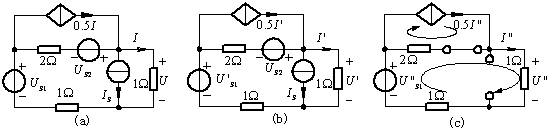
图5 例题3
解:根据已知条件,将电压源![]() 分解成
分解成![]() 。再利用叠加定理,将图(a)电源的作用情况分解成图(b)和图(c)。在图(b)中
。再利用叠加定理,将图(a)电源的作用情况分解成图(b)和图(c)。在图(b)中![]() ,所以
,所以![]() ;图(c)中,只有
;图(c)中,只有![]() 单独作用,对其列回路电流法方程可得
单独作用,对其列回路电流法方程可得
![]()
解得
![]() ,
, ![]()
故题中所求电压
![]()


 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底