第 1 节 动态元件
一、电容元件
电容器是由两块金属极板,中间隔以绝缘介质(如空气、云母、绝缘纸、电解质等)组成,当电容器的两块金属极板之间加以电压时,两块极板上就会聚集等量异性的电荷( charge ),从而建立起电场,储存电场能量,当外加电压撤掉后,极板上的电荷可继续存在,因此,电容器是一种能储存电荷的元件。但是,实际的电容器由于存在介质损耗和漏电流,极板上的电荷会慢慢地消失,时间越长,电荷越少。
1 、伏安特性
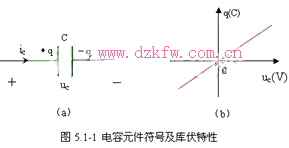
本章讨论的电容元件 ,是在忽略了介质损耗和漏电流等因素之后的理想化模型。电容元件( capacitor )的电路符号如图 5.1-1 ( a )所示。库伏特性为
![]()
其中,电荷量 q 的单位是库仑( coulomb ,简称 C ); C 称为电容元件的电容量,简称电容( capacitance ),单位是法拉( farad ,简称 F ),常用的单位还有微法( uF ),纳法( nF )皮法( pF )等,它们之间的换算关系为
![]()
![]()
电容电压 ![]() 与电流
与电流 ![]() 取非关联参考方向时,电容元件的伏安关系为
取非关联参考方向时,电容元件的伏安关系为![]()
电容元件的特性
1 、动态性
电容上的电流与电压呈微分关系,即任一时刻电容上的电流取决于该时刻电压的变化率,而与该时刻电压本身无关。电压变化越快,电流也就越大,即使某时刻的电压为 0 ,也可能有电流;如果电容两端电压为直流电压( DC voltage ),即电压不随时间的变化而变化,那么电容上就无电流通过,这时电容相当于开路,所以,电容具有隔直流作用。
电容元件的特性
1 、动态性
电容上的电流与电压呈微分关系,即任一时刻电容上的电流取决于该时刻电压的变化率,而与该时刻电压本身无关。电压变化越快,电流也就越大,即使某时刻的电压为 0 ,也可能有电流;如果电容两端电压为直流电压( DC voltage ),即电压不随时间的变化而变化,那么电容上就无电流通过,这时电容相当于开路,所以,电容具有隔直流作用。
3 、储能性
电容元件吸收的瞬时功率为
![]()
若 ![]() ,表明电容吸收电能,电容处于充电( charge )状态;若
,表明电容吸收电能,电容处于充电( charge )状态;若 ![]() ,表明电容释放电能,电容处于放电( discharge )状态。电容从初始时刻
,表明电容释放电能,电容处于放电( discharge )状态。电容从初始时刻 ![]() 到 t 时刻吸收的电能量为
到 t 时刻吸收的电能量为
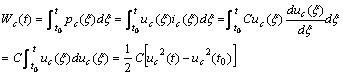
若电容的初始电压 ![]() ,则
,则
![]()
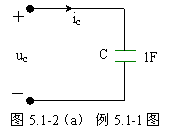
例 5.1-1 图 5.1-2 ( a )所示电路中,电容两端电压 ![]() 的波形如图 5.1-2 ( b )所示。求( 1 )电流
的波形如图 5.1-2 ( b )所示。求( 1 )电流 ![]() 和功率
和功率 ![]() ,并画出它们的波形;( 2 ) t=2s 时电容的储能。
,并画出它们的波形;( 2 ) t=2s 时电容的储能。
|
|
解:( 1 )由图 5.1-2 ( b )所示的波形图可以写出 ![]() 的函数表达式:
的函数表达式:
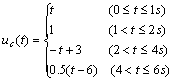
由电容元件的伏安关系,得
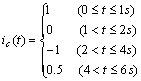
画出 ![]() 的波形,如图 5.1-2 ( c )所示。
的波形,如图 5.1-2 ( c )所示。
电容的瞬时功率为
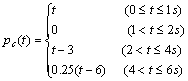
![]() 的单位为 W 。画出
的单位为 W 。画出 ![]() 的波形,如图 5.1-2 ( d )所示。
的波形,如图 5.1-2 ( d )所示。
( 2 ) 由 5.1-2 ( b )可得
t=0 时, ![]()
t=2S 时, ![]()
所以, t=2S 时电容的储能为
![]()
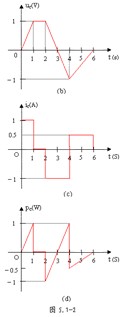
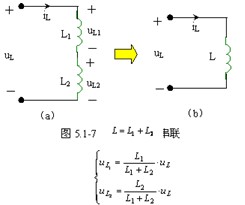
2 、电容元件的串并联
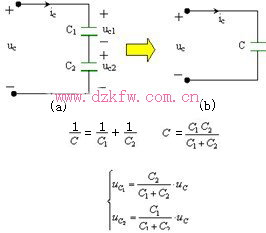
1 )串联
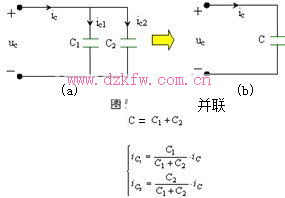
2 )并联
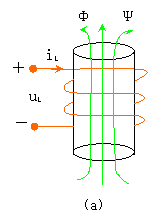
二、电感元件
把金属导线饶在一个铁芯或其它材料上,就构成了一个实际的 电感线圈 ,如图 5.1-5 ( a )所示。当电流 ![]() 通过线圈时,线圈内部或周围就会产生磁场( magnetic field ),并储存磁能量。线圈是由导线饶成的,含有极小的电阻,一般可以忽略。
通过线圈时,线圈内部或周围就会产生磁场( magnetic field ),并储存磁能量。线圈是由导线饶成的,含有极小的电阻,一般可以忽略。
 |
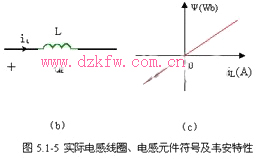
1 、伏安特性
本章讨论的电感元件就是忽略了实际电感线圈的导线电阻等次要因素之后的理想化模型。电感元件的电路符号如图 5.1-5 ( b )所示。当磁链 ![]() 的参考方向与电流
的参考方向与电流 ![]() 的参考方向符合右手螺旋定则时,韦安特性为
的参考方向符合右手螺旋定则时,韦安特性为![]()
磁链的单位是韦伯( Weber ,简称 Wb ); L 称为电感元件的电感量,简称电感( inductance ),单位是亨利( Henry ,简称 H ),常用的单位还有毫亨( mH ),微亨( uH ),它们之间的换算关系![]()
当电感电压与电流为关联参考方向时,其伏安特性为
![]()
当电感电压与电流为非关联参考方向时,其伏安特性为![]()
电感元件的特性
1 、动态性
电感上的电压与电流呈微分关系,即任一时刻电感上的电压取决于该时刻电流的变化率,而与该时刻电流本身无关。电流变化越快,电压也就越大,即使某时刻的电流为 0 ,也可能有电压;如果通过电感的电流为直流电流( DC current ),那么电感上就没有电压,这时电感相当于短路,所以,电感具有通直流作用。
2 、记忆性
任一时刻电感上的电流 ![]() 不仅取决于该时刻的电压
不仅取决于该时刻的电压 ![]() ,而且取决于
,而且取决于 ![]() 所有时间内的电压,即
所有时间内的电压,即 ![]() 与电压的全部历史有关。
与电压的全部历史有关。
![]()
其中 ![]() 称为电感电流的初始值或初始状态,它反映了在
称为电感电流的初始值或初始状态,它反映了在 ![]() 时刻电感上已经积累的电流。
时刻电感上已经积累的电流。
3 、储能性
电感元件吸收的瞬时功率为![]()
若 ![]() ,表明电感从电路中吸收电能,并转化为磁能储存起来;若
,表明电感从电路中吸收电能,并转化为磁能储存起来;若 ![]() ,表明电感将储存的磁能转化成电能,并释放给电路。电感元件从初始时刻
,表明电感将储存的磁能转化成电能,并释放给电路。电感元件从初始时刻 ![]() 到 t 时刻吸收的能量为
到 t 时刻吸收的能量为

如果电感的初始电流 ![]() ,则
,则![]()
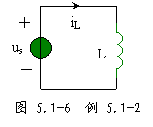
例 5.1-2 图 5.1-6 所示电路中,已知 L=2H ,电压源在 ![]() 时为
时为 ![]() V ,在
V ,在 ![]() 和
和 ![]() 时都为 0 ,求
时都为 0 ,求 ![]() 时电感的储能。
时电感的储能。
 |
解: ![]() 时,电感的电流
时,电感的电流![]()
![]() 时,电感的电流
时,电感的电流
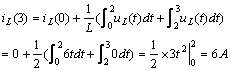
![]() 时电感的储能
时电感的储能
![]()
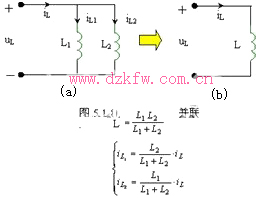
2 、电感元件的串并联
1 )串联
2 )并联


 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底