通信系统都有发送机和接收机,为了提高系统的可靠性,通常在接收机的输入端接有一个带通滤波器,信道内的噪声构成了一个随机过程,经过该带通滤波器之后,则变成了窄带随机过程,因此,讨论窄带随机过程的规律是重要的。
一、窄带随机过程的定义
窄带随机过程的定义借助于它的功率谱密度的图形来说明。图3.5.1(a)中,波形的中心频率为![]() ,带宽为
,带宽为![]() ,当满足
,当满足![]() 时,就可认为满足窄带条件。
时,就可认为满足窄带条件。
若随机过程的功率谱满足该条件则称为窄带随机过程。
若带通滤波器的传输函数满足该条件则称为窄带滤波器。
随机过程通过窄带滤波器之后变成窄带随机过程。
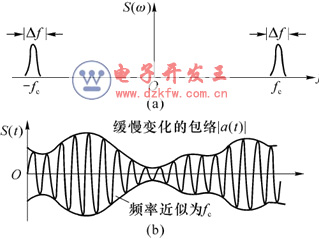
如果在示波器上观察这个过程中一个样本函数的波形,则会发现它像一个包络和相位缓慢变化的正弦波,如图3.5.1(b)所示。因此窄带随机过程可用下式表示成:
窄带随机过程也可用下式表示
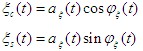
可见,
三、同相分量与正交分量的统计特性
设窄带随机过程是均值为零平稳的窄带高斯过程。可以证明,它的同相分量和正交分量也是均值为零的平稳高斯过程,而且与
1.数学期望
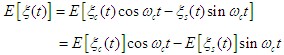
我们知道一些统计特性可以从自相关函数中得到,所以,按定义
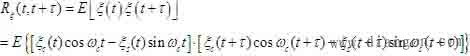
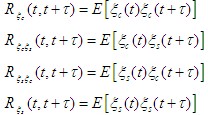
由于式(1)和式(2)相等,则应有
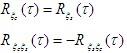
3.概率密度函数
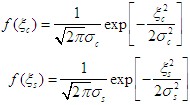
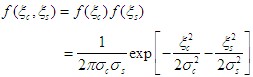
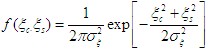
四、包络与相位的统计特性
现在来确定窄带平稳高斯过程的包络和相位的统计特性,随机包络和随机相位可表示为
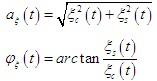
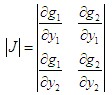
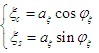
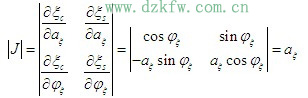
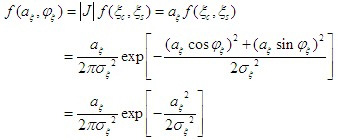
利用概率论中的边际分布知识,可求得包络
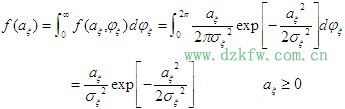
瑞利分布的特点:最大值发生在
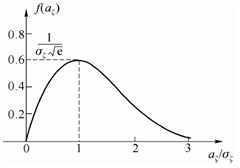
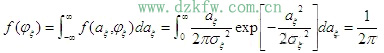
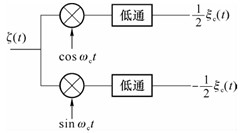
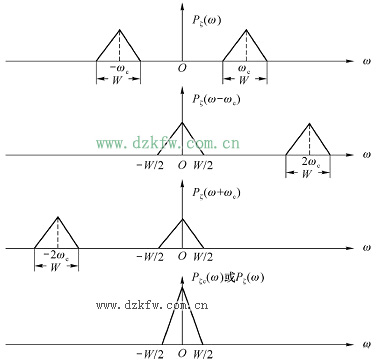
五、窄带随机过程的功率谱密度
结论:窄带随机过程同相分量

证明:窄带随机过程
对式
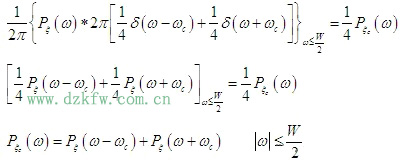
同理,对式
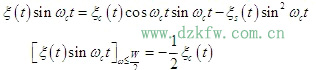



 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底